2026知到答案 概率论与数理统计(青海民族大学) 最新智慧树满分章节测试答案
绪论 单元测试
1、判断题:
袋中装有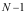 只黑球和
只黑球和![]() 只白球,每次从袋中随机地摸出一只球,并换入一只黑球,这样继续下去,设
只白球,每次从袋中随机地摸出一只球,并换入一只黑球,这样继续下去,设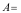 “第
“第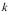 次摸球时得到黑球“,则
次摸球时得到黑球“,则![]() (
( 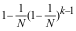 )。( )
)。( )
选项:
A:错
B:对
答案: 【对】
2、判断题:
袋中有5只红球和3只白球。从中任取3只球,已知取出有红球时,那么至多取到1只白球的概率为( 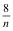 )。( )
)。( )
选项:
A:对
B:错
答案: 【对】
3、判断题:
设两两相互独立的三事件A,B和C满足条件ABC= ,P(A)=P(B)=P(C)<
,P(A)=P(B)=P(C)< 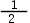 ,且已知P(AUBUC)=
,且已知P(AUBUC)= 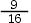 则P(A)=(0.25)。( )
则P(A)=(0.25)。( )
选项:
A:对
B:错
答案: 【对】
第一章 单元测试
1、单选题:
对掷一粒骰子的试验,在概率论中将“出现偶数点”称为( )。
选项:
A:随机事件
B:必然事件
C:样本空间
D:不可能事件
答案: 【随机事件】
2、单选题:
设甲、乙两人进行象棋比赛,考虑事件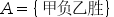 ,则
,则 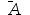 为( )。
为( )。
选项:
A: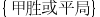
B:
C: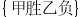
D: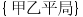
答案: 【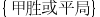 】
】
3、单选题:
设A,B为随机事件,且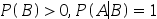 ,则必有( )
,则必有( )
选项:
A:P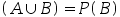
B:P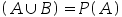
C:P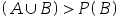
D:P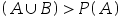
答案: 【P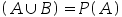 】
】
4、单选题:
设A,B,C 三个事件两两相互独立,则A,B,C相互独立的充要条件是( )
选项:
A:AB与AC独立
B:A与BC相互独立
C:AB与AUC独立
D:AUB与AUC独立
答案: 【A与BC相互独立】
5、单选题:
对于任意两事件A和B,( )。
选项:
A:若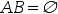 ,则A,B一定独立
,则A,B一定独立
B:若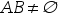 ,则A、B有可能独立
,则A、B有可能独立
C:若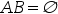 ,则A,B一定不独立
,则A,B一定不独立
D:若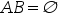 ,则A,B一定独立
,则A,B一定独立
答案: 【若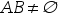 ,则A、B有可能独立】
,则A、B有可能独立】
6、单选题:
将一枚硬币独立地掷两次,引进事件: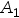 =“掷第一次出现正面”,
=“掷第一次出现正面”,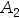 =“第二次出现正面”,
=“第二次出现正面”,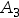 =“正、反面各出现一次”,
=“正、反面各出现一次”,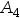 =“正面出现两次”,则事件( )。
=“正面出现两次”,则事件( )。
选项:
A: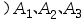 两两独立
两两独立
B: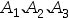 相互独立
相互独立
C: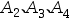 相互独立
相互独立
D: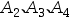 两两独立
两两独立
答案: 【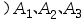 两两独立】
两两独立】
7、单选题:
设两个随机事件A与B相互独立,且P( )=0.5,P(A-B)=0.3,则P(B-A)=( )。
选项:
A:0.3
B:0.2
C:0.4
D:0.1
答案: 【0.2】
8、单选题:
若A,B为任意两个随机事件,则( )。
选项:
A: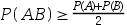
B:)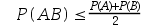
C: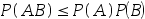
D: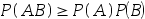
答案: 【)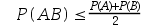 】
】
9、单选题:
设A,B为两个随机事件,且0<P(A)<1,0<P(B)<1,如果P(A|B)=1,则( )。
选项:
A: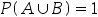
B: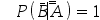
C: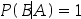
D: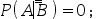
答案: 【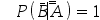 】
】
10、单选题:
设有10个零件,其中2个是次品,现随机抽取2个,恰有一个是正品的概率( )。
选项:
A: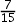
B: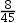
C: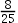
D: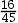
答案: 【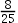 】
】
第二章 单元测试
1、单选题:
对于随机变量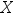 ,函数
,函数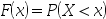 称为
称为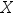 的( )。
的( )。
选项:
A:分布函数
B:概率分布
C:概率
D:概率密度
答案: 【分布函数】
2、单选题:
设随机变量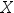 的分布函数为
的分布函数为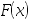 ,在下列概率中可表示为
,在下列概率中可表示为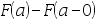 的是( )。
的是( )。
选项:
A: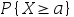
B: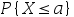
C: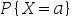
D: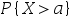
答案: 【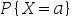 】
】
3、单选题:
设随机变量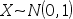 ,则X的分布函数
,则X的分布函数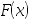 满足( )。
满足( )。
选项:
A: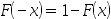
B: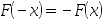
C: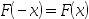 )
)
D: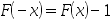
答案: 【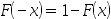 】
】
4、单选题:
设随机变量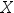 的密度函数为
的密度函数为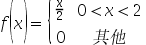 ,则
,则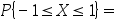 ( )。
( )。
选项:
A:0.25
B:1
C:0.5
D:0
答案: 【0.25】
5、单选题:
设随机变量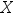 的密度函数
的密度函数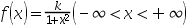 ,则
,则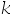 的值是( )。
的值是( )。
选项:
A: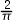
B:
![]()
C: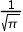
D: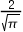
答案: 【
![]()
】
6、单选题:
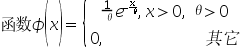 是( )的概率密度。
是( )的概率密度。
选项:
A:指数分布
B:均匀分布
C:正态分布
D:泊松分布
答案: 【指数分布】
7、单选题:
当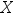 服从参数为
服从参数为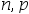 的二项分布时,
的二项分布时,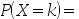 ( )。
( )。
选项:
A: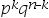
B: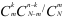
C: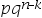
D: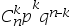
答案: 【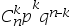 】
】
8、单选题:
设离散型随机变量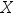 的分布列为
的分布列为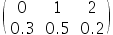 ,其分布函数为
,其分布函数为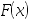 ,则
,则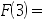 ( )。
( )。
选项:
A:0.8
B:0
C:0.3
D:1
答案: 【1】
9、单选题:
设随机变量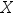 的密度函数为
的密度函数为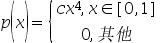 ,则常数
,则常数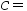 ( )。
( )。
A . 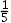
选项:
A:4
B:5
C: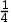
答案: 【5】
10、判断题:
如果设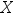 ~
~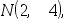 那么
那么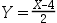 ~
~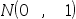 。 ( )
。 ( )
选项:
A:对
B:错
答案: 【错】
11、判断题:
设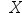 ~
~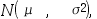 那么
那么 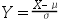 ~
~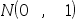 。 ( )
。 ( )
选项:
A:对
B:错
答案: 【对】
